
ども!
ライフコーチ 兼 ド底辺サラリーマンのけんいちです。
突然ですが、フィボナッチ数列ってご存知ですか?
僕は株のトレードをしているので、そこで初めて知りました。
ある一定の法則で並ぶ数列のことなのですが、数学の分野だけではなく世の中にはこの法則に従ったものがたくさんあるのです。
ヒマワリの種の数や、巻貝のうずまきの角度など、人の手が加えられてない自然界にもこの法則が多く当てはまるものがあり、非常に神秘的で面白い!
数学が苦手で嫌いだった僕でもめちゃくちゃワクワクしました!
そんな僕みたいな人に、フィボナッチ数列とは何かを概要だけザックリお伝えします。
これを知ったからといって何か手に入るわけではないです(笑)
ただ、自然界を支配するこの数列を知ると、「美しい」と思える比率である「黄金比」などもわかるので何か生み出すようなアーティストの方には役に立つかもしれません。
なにより、株をやってる人はチャート分析にとても大切ですよ!
それでは早速解説していきます!
(約4分で読めます)
フィボナッチ数列って何?

フィボナッチ数列とは、12世紀後半〜13世紀に生きた「レオナルド・フィボナッチ」というイタリアの数学者が発見した法則です。

3項目以降のそれぞれの数は手前の2つの項の数の和になっている。
「何言ってるのかようわからん!」って人が多いと思うので(笑)実際の数列で見てみましょう。
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377...
数列の3番目は1ですね。これは0+1=1。
数列の4番目は2ですから、1+1=2になります。
このように、数列の数字は1つ前と2つ前を足した数になるという法則です。
これはどんな数字を入れても当てはまります。
こうした法則があることを発見したのがフィボナッチさんで、フィボナッチ数列と名付けられました。
法則を見つけるだけでもまぁすごいのですが、これのなにがすごいって自然界ではこの法則に従ってるものばかりなのです。
たとえば、ヒマワリの種。
ヒマワリの種はびっしり不規則に詰まっていそうですが、実はフィボナッチ数列のように均等になってるのです。

左と右にそれぞれ螺旋状になってますが、
左回りに21列、右回りに34列になってたり、左回りに34列、右回りに55列になっていたりフィボナッチ数列が当てはまるのです!
それもすべてです。
他にも有名なところでいうと、貝のらせん状のうずまきもそうです。
まず、フィボナッチ数列通りの図形を書いていくと以下の通りになります。
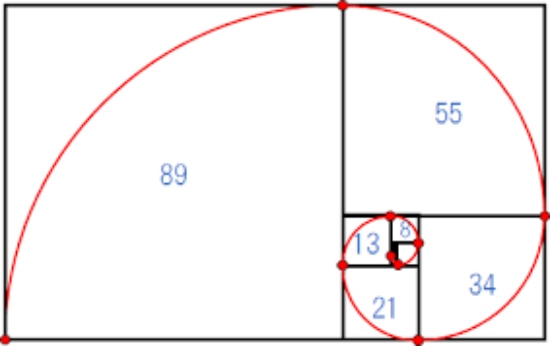
フィボナッチ数列に従って、8の隣は、8+5の13cmの正方形を書き、その隣には、13+8の21cmの図形を書いて、その隣には....とうずまきのように中心から書いていくと、綺麗な図形が出てくるのです。
そして中心から円を描くようにすると、貝のうずまきに似ていますね。
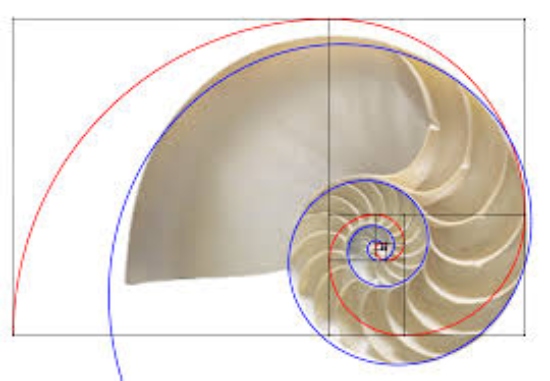
なんとこのように貝の巻き具合もフィボナッチ数列に従っていたのです!
いやーーー不思議ですよね!!
偶然ではなく自然界の法則のようにも感じます。
他にも松ぼっくりなどもフィボナッチ数列に従っているそうです。
興味のある方はいろいろと調べてみてください(^^♪
フィボナッチ数列を学ぶメリット

「でも、そんなの学んだって何のためになるの~?」
という方もいるかと思います。
具体的なためになる事例は後述しますが、僕は単純に「知らないものを知る」ということにそもそも意義があると感じてます。
普段の生活に役に立つかというと、ぶっちゃけ普段は使いません(笑)
でも、こういう法則があるんだ~と知っておくのは、知らないのと比べると断然いいですよね。
知的好奇心がくすぐられませんか?!笑
自然界の法則だとしたら、、、、
我々の生命にも何か通ずるものあるかもしれません。
少なくとも、わたしたちが「美しい」と感じるものにフィボナッチ数列が絡んでいることがわかっています。
黄金比である1:1.6というのもフィボナッチ数列が関係しています。
それも後述します。
フィボナッチ数列が役に立つ事例
フィボナッチ数列が役に立つ事例を紹介します。
エコシャワーヘッド

アメリカの会社は、ひまわりの種をヒントに、らせん状にフィボナッチ数列に従って水が出る穴を配置したところ、スキマなく水が出るようなシャワーを開発出来ました。
黄金比
さきほどの、画像をもう一度持ってきます。

これ、正方形で形作られた長方形となっていますが、タテとヨコの長さを見てみましょう。
タテ89cmでヨコは144cm。比率で言うと、1:1.6(厳密には1.6179・・・)になるのです。
どの数字を当てはめても、限りなく1:1.6に近い数字になります。
人は、1:1.6の対比が美しいと感じるのです。
有名なところではギリシアのパルテノン神殿。

1:1.6に近しい比率で作られています。
当時の人たちが、この法則を知っていたかどうかはわかりませんが、この比率が「美しい」と感じるということにはもしかしたら気づいていたのかもしれませんね。
レオナルドダヴィンチの『モナリザ』の顔も1:1.6となっています。

このように、フィボナッチ数列は、芸術作品を創出する人には、知っておくべき法則です!
株のチャート分析
僕含めてトレーダーの方なら皆さんご存知のフィボナッチ数。
要は、8、13、21といったフィボナッチ数で価格の動きに変化が起きると言われているのです。
よく使われるのは、61.8という数字。
これは100÷61.8=1.61812・・・・という数字でフィボナッチ数列で出てくる1.6という数字です。
以下の画像がわかりやすかったので、引用させてもらいました。
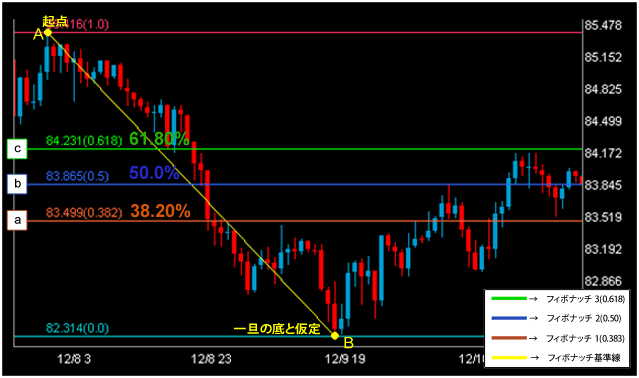
A地点を起点とし、株価が下落していて、B地点で反転して上昇している状況です。
緑色のラインのフィボナッチ61.8%をみてみましょう。
Aを0とし、Bを100としたときの61.8%のラインでまた押し戻されていますね。
こういう現象がよくあるのです。
不思議ですね。
株を買っている人、売っている人たちがひとつ意識する指標になっているのでしょう。
株価は買う人が多ければ上昇し、売る人が多ければ下落します。
フィボナッチ数列の法則に、買う人売る人は影響されているのです。
フィボナッチ数列は面白い!

フィボナッチ数列の面白さと不思議な魅力を感じてもらえたでしょうか。
自然界にこんなにも多くフィボナッチ数列の法則に従ったものがあふれていて、また、人間が「美しい」と感じる黄金比もフィボナッチ数列から来ているのです。
芸術家には知っておくべき知識だし、僕のような株のトレーダーにも必須の知識です。
それだけではなくこんなにも多くのもの関わっているのだから、誰でも知っておいて損はないでしょう!
最後に、面白い黄金比をお見せします。
これもネットで見つけました(^^♪
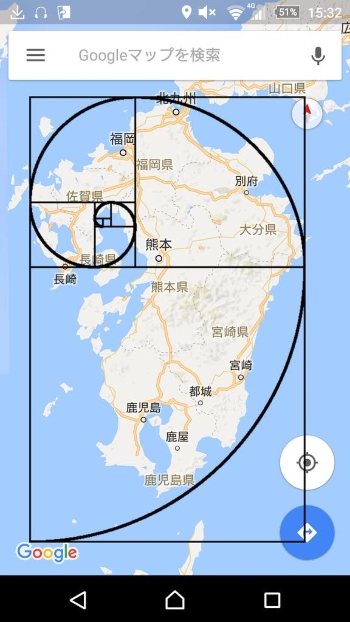
なんと!九州もフィボナッチ数列に従った黄金比!!笑
九州って確かに形きれいですよね。
フィボナッチ数列に魅了された人は以下の本がオススメ!笑
フィボナッチ数列だけではなく、ピラミッドに隠された黄金比なども書かれています!
また、フェルマーの最終定理という数学の歴史上もっとも難解だと言われている定理についても書かれていて、数学好きの人じゃなくても知的好奇心をくすぐられるハズ!
最後までお読みいただきありがとうございました!
ではまた。
ざす。
